ONDAS MECÁNICAS

Conceptos Previos

Introducción a las Ondas

Las ondas que se producen en un estanque, los sonidos musicales y los movimientos causados por un terremoto son fenómenos ondulatorios. Las ondas se generan cuando se perturba el estado de equilibrio de un sistema, y tal perturbación viaja o se propaga de una región del sistema a otra.
Al propagarse una onda, transporta energía. La energía de las ondas de la luz solar calienta la superficie terrestre, en tanto que la energía de las ondas sísmicas puede agrietar la corteza de nuestro planeta.

En este capítulo se profundizará el estudio de las ondas mecánicas, ondas que viajan por un material llamado medio. Iniciaremos este capítulo deduciendo las ecuaciones básicas que describen las ondas, incluyendo el importante caso especial de las ondas sinusoidales donde el patrón de la onda es una función repetitiva seno o coseno.

Ondas Mecánicas

Definición de Onda Mecánica

Una onda mecánica es una perturbación que viaja a través de un material o una sustancia que es el medio de la onda. Al viajar la onda por el medio, las partículas que constituyen el medio experimentan desplazamientos de varios tipos, según la naturaleza de la onda.

Clasificación de las Ondas Mecánicas

Las ondas mecánicas se pueden clasificar en:

• Ondas Transversales: Las partículas del medio se desplazan perpendicularmente a la dirección en que la onda viaja por el medio.
• Ondas Longitudinales: Las partículas del medio se desplazan en la misma dirección en que viaja la onda.

Ondas Periódicas

Definición de Onda Periódica

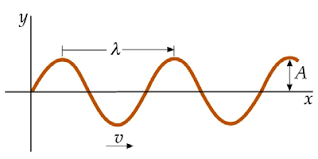
Una onda periódica es aquella en la que la perturbación que la origina se repite a intervalos regulares de tiempo. Un caso especial de onda periódica es la onda sinusoidal, donde el patrón de la onda es una función seno o coseno.

Función de Onda Sinusoidal

La función de onda para una onda sinusoidal que se propaga en la dirección positiva del eje \( x \) es:

\( y(x,t) = A \cos (kx - \omega t) \)

donde:

• \( A \) es la amplitud de la onda.
• \( k \) es el número de onda, \( k = \frac{2\pi}{\lambda} \).
• \( \omega \) es la frecuencia angular, \( \omega = 2\pi f \).
• \( \lambda \) es la longitud de onda.
• \( f \) es la frecuencia de la onda.
• \( t \) es el tiempo.
• \( x \) es la posición.

Rapidez de una Onda Periódica

La rapidez \( v \) de una onda periódica está dada por la relación:

\( v = \lambda f \)

Esto significa que la rapidez de propagación de la onda es el producto de su longitud de onda y su frecuencia.

Propagación de Ondas en una Cuerda

Para una onda transversal que se propaga en una cuerda, la rapidez de la onda \( v \) depende de la tensión \( F \) en la cuerda y de la masa por unidad de longitud \( \mu \):

\( v = \sqrt{\frac{F}{\mu}} \)

Descripción Matemática de una Onda

Muchas características de las ondas periódicas pueden describirse usando los conceptos de rapidez, amplitud, periodo, frecuencia y longitud de onda; sin embargo, es común que necesitemos una descripción más detallada de las posiciones y los movimientos de las partículas individuales del medio en determinados instantes durante la propagación de la onda.

Función de Onda

La posición de una partícula en una cuerda que oscila con una onda sinusoidal está descrita por la función de onda:

\( y(x,t) = Acos(kx- \omega t) \)

Velocidad y Aceleración de las Partículas

La velocidad transversal de una partícula en una onda transversal se obtiene derivando la función de onda con respecto al tiempo:

\( v_y(x, t) = -A \omega \sin (kx - \omega t) \)

La aceleración transversal de una partícula se obtiene derivando la velocidad con respecto al tiempo:

\( a_y(x, t) = -A \omega^2 \cos (kx - \omega t) \)

Ecuación de Onda

La ecuación de onda relaciona las segundas derivadas parciales de la función de onda con respecto a \( x \) y \( t \):

\( \frac{\partial^2 y}{\partial t^2} = v^2 \frac{\partial^2 y}{\partial x^2} \)

Esta ecuación indica que cualquier perturbación en la cuerda se propagará a una rapidez \( v \) que depende de las propiedades del medio.

Número de Onda y Frecuencia Angular

Es conveniente definir una cantidad \( k \) llamada número de onda y la frecuencia angular \( \omega \):

\( k = \frac{2\pi}{\lambda} \) \( \omega = 2\pi f \)

Podemos reescribir la función de onda en términos del número de onda y la frecuencia angular:

\( y(x, t) = A \cos(kx - \omega t) \)

Ondas Transversales en una Cuerda

Las ondas transversales en una cuerda son un ejemplo importante de ondas mecánicas. Consideremos una cuerda perfectamente flexible con tensión \( F \) y densidad lineal de masa \( \mu \). La rapidez de una onda transversal en esta cuerda está dada por:

\( v = \sqrt{\frac{F}{\mu}} \)

Derivación de la Rapidez de Onda

Para deducir la expresión para la rapidez de onda, observamos que todas las partículas de la parte en movimiento de la cuerda se mueven hacia arriba con velocidad constante \( v_y \), pero no con aceleración constante. Aplicando la segunda ley de Newton a un pequeño segmento de cuerda, cuya longitud en la posición de equilibrio es \( \Delta x \), obtenemos:

\( F_y = F \left( \left. \frac{\partial y}{\partial x} \right|_{x+\Delta x} - \left. \frac{\partial y}{\partial x} \right|_x \right) \)

Igualando esto a la masa del segmento multiplicada por la aceleración transversal, obtenemos la ecuación de onda:

\( \frac{\partial^2 y}{\partial x^2} = \frac{\mu}{F} \frac{\partial^2 y}{\partial t^2} \)

De aquí deducimos que la rapidez de propagación de la onda es:

\( v = \sqrt{\frac{F}{\mu}} \)

Ejemplo de Cálculo de la Rapidez de Onda

Supongamos que tenemos una cuerda con una tensión de 50 N y una densidad lineal de masa de 0.1 kg/m. La rapidez de una onda transversal en la cuerda es:

\( v = \sqrt{\frac{50}{0.1}} = \sqrt{500} = 22.36 \, \text{m/s} \)

Ondas Longitudinales

Descripción de una Onda Longitudinal

Para una onda longitudinal que se propaga en un tubo lleno de fluido, con un pistón que oscila en un extremo, la función de onda es similar a la de una onda transversal, pero el desplazamiento es paralelo al eje del tubo:

\( y(x, t) = A \cos (kx - \omega t) \)

Las regiones de compresión y rarefacción se mueven a lo largo del tubo, y la longitud de onda es la distancia entre dos compresiones sucesivas.

Rapidez de una Onda Longitudinal

La rapidez de una onda longitudinal en un fluido depende de las propiedades elásticas del fluido y de su densidad. En el caso de ondas sonoras en el aire, la rapidez está dada por:

\( v = \sqrt{\frac{B}{\rho}} \)

donde \( B \) es el módulo de elasticidad volumétrica del fluido y \( \rho \) es la densidad del fluido.

Ejemplo de Onda Sonora

Calculemos la longitud de onda de una onda sonora en el aire a 20°C, si la frecuencia es de 262 Hz (la frecuencia aproximada del do central de un piano). La rapidez del sonido a 20°C es de 344 m/s.

\( \lambda = \frac{v}{f} = \frac{344}{262} = 1.31 \, \text{m} \)

Interferencia y Superposición de Ondas

Principio de Superposición

Cuando dos o más ondas se encuentran en un punto, la perturbación resultante es la suma algebraica de las perturbaciones individuales. Este principio se conoce como el principio de superposición.

Interferencia Constructiva y Destructiva

Dependiendo de las fases relativas de las ondas que se superponen, podemos tener interferencia constructiva o destructiva:

• Interferencia Constructiva: Ocurre cuando las crestas de una onda se alinean con las crestas de otra, resultando en una onda de mayor amplitud.
• Interferencia Destructiva: Ocurre cuando las crestas de una onda se alinean con los valles de otra, resultando en una disminución de la amplitud.

Ondas Estacionarias

Las ondas estacionarias se forman cuando dos ondas de la misma frecuencia y amplitud se propagan en direcciones opuestas y se superponen. En una onda estacionaria, ciertos puntos llamados nodos permanecen en reposo, mientras que los antinodos son puntos de máxima amplitud.

Fórmulas de Ondas Estacionarias

La longitud de onda de las ondas estacionarias en una cuerda fija en ambos extremos está dada por:

\( \lambda = \frac{2L}{n} \)

donde \( L \) es la longitud de la cuerda y \( n \) es el número de armónicos. La frecuencia de las ondas estacionarias está dada por:

\( f_n = \frac{n}{2L} \sqrt{\frac{F}{\mu}} \)

Ondas en Instrumentos Musicales

Cuerdas Vibrantes

Los instrumentos de cuerda como la guitarra o el violín producen ondas que viajan en direcciones opuestas a lo largo de las cuerdas del instrumento. Al superponerse estas ondas, se genera interferencia y se forman ondas estacionarias con frecuencias específicas llamadas frecuencias de modo normal.

Ondas en Tubos de Aire

Los instrumentos de viento como las flautas y los órganos de tubos también producen ondas estacionarias. En estos instrumentos, el aire en el tubo vibra con ciertas frecuencias específicas determinadas por la longitud del tubo y la velocidad del sonido en el aire.

Fórmulas para Instrumentos de Viento

Para un tubo cerrado en un extremo, las frecuencias de resonancia están dadas por:

\( f_n = \frac{(2n-1)v}{4L} \)

donde \( n \) es un número entero positivo, \( v \) es la velocidad del sonido y \( L \) es la longitud del tubo.

Ondas Electromagnéticas

Definición de Onda Electromagnética

Las ondas electromagnéticas son ondas que no requieren un medio material para propagarse. Incluyen la luz visible, las ondas de radio, las radiaciones infrarroja y ultravioleta, y los rayos X.

Propagación en el Vacío

Las ondas electromagnéticas se pueden propagar en el vacío. La rapidez de propagación de las ondas electromagnéticas en el vacío es igual a la velocidad de la luz, \( c \):

\( c = 3 \times 10^8 \, \text{m/s} \)

Ecuación de Maxwell

Las ecuaciones de Maxwell describen la propagación de las ondas electromagnéticas. La forma de onda de una onda electromagnética puede representarse como:

\( E(x, t) = E_0 \cos (kx - \omega t) \) \( B(x, t) = B_0 \cos (kx - \omega t) \)

donde \( E \) es el campo eléctrico y \( B \) es el campo magnético.

Conclusión

Las ondas mecánicas y electromagnéticas son fundamentales en la física y tienen aplicaciones en diversas áreas, desde la música hasta la comunicación y la medicina. La comprensión de las propiedades y el comportamiento de las ondas es esencial para el desarrollo de tecnologías avanzadas y la mejora de nuestras capacidades de percepción y análisis del entorno.