La dinámica de un sistema de partículas
es un área fundamental en la física que
estudia el movimiento de varias partículas
interaccionando entre sí. Este campo es
esencial para comprender cómo objetos en el
universo se mueven y cambian con el tiempo.
Cantidad de movimiento de un Sistema de Partículas
Se tiene un sistema de partículas, donde todas las partículas
se mueven con una velocidad diferente, simultáneamente al mismo momento.
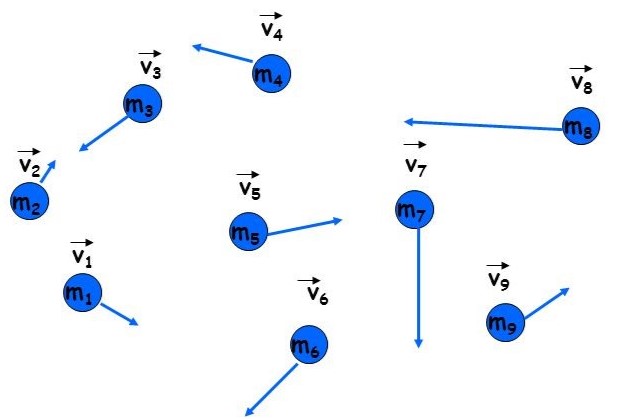
Para hallar la cantidad de movimiento del sistema de partículas, sumaremos todas las cantidades de movimiento
de cada partícula.
\( \vec{p}=m.\vec {v} \frac {kg.m}{s} \)
\( \vec{p}_{sp}=\sum_{i=1}^{n} \vec{p}_i = \vec{p}_1+\vec{p}_2+\vec{p}_3+...+\vec{p}_n \)
Impulso de una fuerza
El impulso es un término que cuantifica el efecto general
de una fuerza que actúa con el tiempo. Se define como la integral de la función fuerza con respecto al tiempo.
\( \vec{I}_{t_1 \rightarrow t_2}^{\vec{F}} = \int_{t_1}^{t_2} F(t)\,dt \)
Caso Particular:
\( \vec{I}_{t_1 \rightarrow t_2}^{\vec{F}}=\vec{F} \Delta t \)
Donde \( \Delta t= t_2 - t_1 \)

Impulso de una fuerza resultante
El impulso de una fuerza
resultante, se vincula con
la variación de la cantidad
de movimiento. Esto se
demuestra de la siguiente
manera:
Primero por segunda ley de Newton:
\( \sum \vec{F}=\vec{F}_{res}=m.\vec{a} \)......(1)
La aceleracion se expresa como:
\( \vec{a}=\frac{\vec{v}_f-\vec{v}_i}{\Delta t} \)......(2)
Reemplazando (2) en (1):
\( \vec{F}_{res}=m.\vec{a}=m.\frac{\vec{v}_f-\vec{v}_i}{\Delta t}\)
\(=\frac{m\vec{v}_f-m\vec{v}_i}{\Delta t}=\frac{\vec{p}_f-\vec{p}_i}{\Delta t} =\frac{\Delta \vec{p}}{\Delta t} \).....(3)
Ahora, el impulso de la fuerza resultante
se expresa como:
\(\vec{I}_{t_1 \rightarrow t_2}^{\vec{F}_{res}}=\vec{F}_{res}.\Delta t \).....(4)
Reemplazando (3) en (4):
\( \vec{F}_{res}.\Delta t=\frac{\vec{p}_f-\vec{p}_i}{\Delta t}.\Delta t=\vec{p}_f-\vec{p}_i=\Delta \vec{p} \)
Por lo tanto:
\( \vec{I}_{t_1 \rightarrow t_2 }^{\vec{F}_{res}}=\Delta \vec{p} \)
Ésta va a ser otra forma alternativa
de expresar la segunda Ley de Newton, en este caso
para fuerzas que dependen del tiempo.
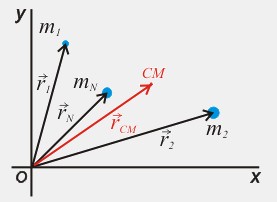
Centro de Masa de un Sistema de Partículas
El centro de masa de un sistema de partículas
es un punto que, a muchos efectos, se mueve como
si fuera una partícula de masa igual a la masa
total del sistema sometida a la resultante de varias
fuerzas que actúan sobre el mismo.
Para calcular el centro de masa de un sistema de
partículas, disponemos un sistema de coordenadas
y tener el vector posicion de cada particula.
El vector centro de masa se hallará
de la siguiente manera:
\(\vec{r}_{CM}=\frac{m_1.\vec{r}_1+m_2.\vec{r}_2+...+m_n.\vec{r}_n}{m_1+m_2+...+m_n} \)
Sea \( M=m_1+_2+...+m_n \) por lo tanto:
\(\vec{r}_{CM}=\frac{1}{M}.\sum_{i=1}^{n}m_i.\vec{r}_i=\frac{1}{M}\int p\,dv\vec{r} \)
Para hallar la velocidad del centro de masa, consideraremos que cada
partícula tiene un vector velocidad.
\( \vec{v}_{CM}=\frac{1}{M}\sum_{i=1}^{n}m_i.\vec{v}_i \)
Recordemos que por definición:
\( \vec{p}=m.\vec{v} \)
\( \vec{p}_{total}=\sum_{i=1}^{n}m_i.\vec{p}_i \)
Por lo tanto la velocidad del centro de masa
se expresa de la siguiente manera:
\( \vec{p}_{CM}=\vec{v}_{CM}.M \)
También se puede expresar de la siguiente manera:
\( \vec{v}_{CM}=\frac{1}{M}\int p\,dv.\vec{v} \)
Para hallar la aceleración del centro de masa,
consideraremos que cada partícula tiene un vector
aceleración:
\( \vec{a}_{CM}=\frac{1}{M}.\sum_{i=1}^{n}m_i.\vec{a}_i=\frac{1}{M}\int p\, dv.\vec{a} \)
Y en el dinámico:
\( \vec{F}_{Resultante}=\vec{F}_{Resultante Externa} \)
\(= \frac{d}{dt}\vec{p}=\frac{d}{dt}M.\vec{v}_{CM}=M.\vec{a}_{CM} \)
Por lo tanto
\( \vec{F}_{R.EXT.}=M.\vec{a}_{CM} \)
Con este resultado, se puede inferir que el sistema de
partículas puede reemplazarse por una partícula con la masa
del SP, M, moviéndose según rcm
Energía de un Sistema de Partículas
Energía Cinética de un Sistema de Partículas
\( E_{K(SP)}=E_{K(CM)} +\sum_{i=1}^{n}E_{Ki}\)
\( =\frac{1}{2}v_{CM}M+\frac{1}{2}\sum_{i=1}^{n}m_i.v_{i}^{2} \)
Donde:
\( E_{K(SP)} \):Energía Cinética del SP
\( \sum_{i=1}^{n}E_{Ki} \):Sumatoria de las energías cinéticas de cada componente del sistema.
Energía Potencial de un Sistema de Partículas
Energía Mecanica de un Sistema de Partículas