DINÁMICA DEL MOVIMIENTO DE ROTACIÓN
Definición de Cuerpo Rígido
(1) Cuerpo ideal cuyas partes (partículas que lo forman) tienen posiciones relativas fijas, entre sí cuando se somete a fuerzas externas, es decir es no deformable. Con esta definición se elimina la posibilidad de que el objeto tenga movimiento de vibración.

(2) Es un cuerpo donde sus dimensiones no se pueden despreciar y mantienen su forma y tamaño cuando son sometidos a fuerzas y con ello la distancia entre dos puntos del cuerpo se mantienen constante. (pueden incluso tener movimiento de traslación y rotación)
Definición de Movimiento de Rotación Pura
Cuando un cuerpo rígido realiza un movimiento de rotación pura todos sus puntos realizan desplazamientos angulares iguales respecto al eje de rotación.
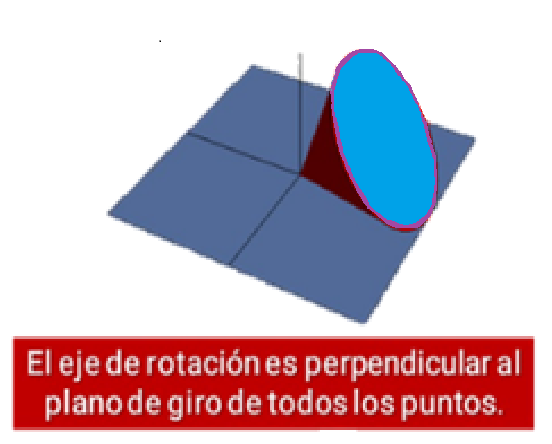
Definición de Torca
Puedes conocerla con otros nombres como:
- Momento de Fuerza
- Momento de Giro
- Par Torsor
- Momento de torsión
- Par motor (en el contexto de motores y maquinaria)
Sabemos que las fuerzas que actúan sobre un cuerpo pueden afectar su movimiento de traslación, es decir, el movimiento del cuerpo como un todo en el espacio. Ahora queremos aprender qué aspectos de una fuerza determinan qué tan efectiva es ésta para provocar o modificar el movimiento de rotación. La magnitud y la dirección de la fuerza son importantes, al igual que el punto de su aplicación sobre el cuerpo.
Cuando un cuerpo rígido realiza un movimiento de rotación pura todos sus puntos realizan desplazamientos angulares iguales respecto al eje de rotación.
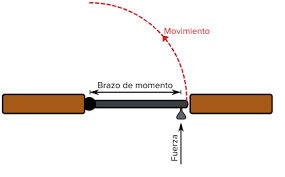
La torca es una medida cuantitativa de la tendencia de una fuerza para provocar o modificar el movimiento de rotación de un cuerpo. Decimos que una fuerza genera una torca sobre un punto específico. En general, la torca para una fuerza de magnitud \( F \) cuya línea de acción es una distancia perpendicular \( l \) desde el punto de rotación es:
\( \tau = F \cdot l \)
La torca también puede calcularse utilizando el producto vectorial:
\( \tau = \vec{r} \times \vec{F} \)
Donde:
- \( \tau \) es la torca
- \( \vec{r} \) es el vector de posición
- \( \vec{F} \) es la fuerza
La torca es fundamental para entender el comportamiento de sistemas mecánicos. En ingeniería y física, el cálculo preciso de la torca es crucial para diseñar mecanismos que puedan soportar fuerzas específicas sin fallar.
Fórmulas de Torca
La fórmula general para la torca es:
\( \tau = \vec{r} \times \vec{F} \)
Dónde:
- \( \tau \) es la torca
- \( \vec{r} \) es el vector de posición
- \( \vec{F} \) es la fuerza
La torca también puede calcularse usando el brazo de palanca:
\( \tau = F \cdot l \cdot \sin(\theta) \)
Dónde:
- \( F \) es la magnitud de la fuerza
- \( l \) es la longitud del brazo de palanca
- \( \theta \) es el ángulo entre el brazo de palanca y la dirección de la fuerza
El concepto de brazo de palanca es fundamental para el diseño de herramientas y máquinas. Por ejemplo, en una llave inglesa, el largo del mango actúa como un brazo de palanca que amplifica la fuerza aplicada para generar una torca mayor.
EQUILIBRIO DE CUERPO RÍGIDO
Como el cuerpo rígido puede trasladarse o rotar, existen condiciones de equilibrio para cada uno de esos movimientos y ambas deben cumplirse
Primera condición de equilibrio
Realizado el DCL: \(\vec{F}_{\text{Resultante}} = \sum \vec{F} = \vec{0}\)
Segunda condición de equilibrio
Elegido un eje: \(\vec{\tau}_{\text{Resultante}} = \sum \vec{\tau} = \vec{0}\)
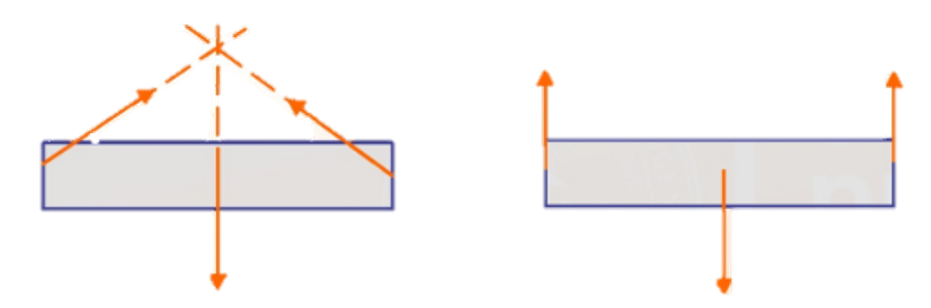
Si un cuerpo rígido en equilibrio mecánico está sometido a tres fuerzas coplanares, estas o son concurrentes o son paralelas.
Trabajo y Potencia en Movimiento de Rotación
En el movimiento de rotación, el trabajo realizado por una fuerza es:
\( W = \tau \theta \)
Y la potencia es:
\( P = \tau \omega \)
Dónde:
- \( W \) es el trabajo
- \( \tau \) es la torca
- \( \theta \) es el ángulo de rotación
- \( P \) es la potencia
- \( \omega \) es la velocidad angular
El trabajo en el movimiento de rotación se puede entender de manera similar al trabajo en el movimiento lineal. Si aplicamos una torca a un cuerpo, estamos realizando trabajo sobre ese cuerpo, y la cantidad de trabajo realizado está dada por el producto de la torca y el ángulo a través del cual se aplica la torca.
La potencia en el movimiento de rotación es la tasa a la cual se realiza trabajo. Es decir, es la cantidad de trabajo realizado por unidad de tiempo. Al igual que en el movimiento lineal, la potencia se puede calcular como el producto de la torca y la velocidad angular del cuerpo.
En los motores eléctricos, la potencia y el trabajo rotacional son conceptos esenciales. Un motor convierte energía eléctrica en energía mecánica rotacional, y su eficiencia depende de cuán efectivamente puede convertir esa energía y transmitirla a una carga.
Momento Angular
El momento angular es una cantidad vectorial que representa el estado de rotación de un objeto. Se define como el producto del momento de inercia y la velocidad angular. Para un cuerpo rígido que gira alrededor de un eje fijo, el momento angular se expresa como:
\( L = I \omega \)
Dónde:
- \( L \) es el momento angular
- \( I \) es el momento de inercia
- \( \omega \) es la velocidad angular
El momento angular de un sistema de partículas se calcula sumando los momentos angulares individuales de todas las partículas. En el caso de un cuerpo rígido, esto se simplifica ya que todas las partículas del cuerpo tienen la misma velocidad angular.
El momento angular es crucial para comprender el comportamiento de sistemas en rotación, como los planetas en el sistema solar. Su conservación explica por qué los planetas siguen órbitas estables y por qué los cuerpos en rotación tienden a mantener su orientación.
Conservación del Momento Angular
El principio de conservación del momento angular establece que si no hay una torca neta externa actuando sobre un sistema, el momento angular total del sistema permanece constante. Este principio es fundamental en muchos fenómenos físicos, desde el movimiento de los planetas hasta el comportamiento de los patinadores artísticos.
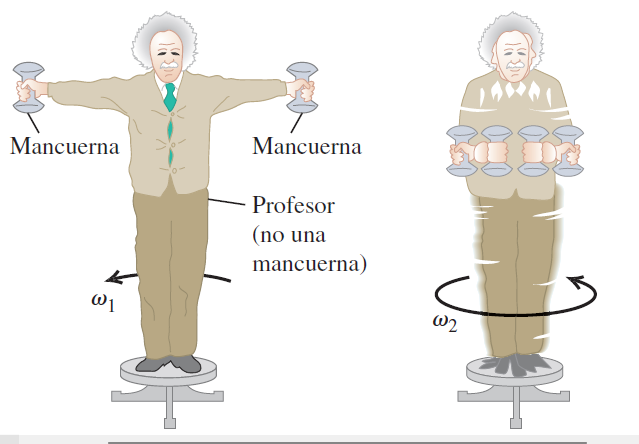
Un ejemplo común de conservación del momento angular es un patinador sobre hielo que gira con los brazos extendidos y luego los recoge. Al hacerlo, su velocidad de rotación aumenta para conservar el momento angular. Este fenómeno se debe a que el momento de inercia disminuye cuando el patinador recoge los brazos, por lo que la velocidad angular debe aumentar para mantener el producto \( L = I \omega \) constante.
La conservación del momento angular también se aplica en sistemas astrofísicos. Por ejemplo, las estrellas en colapso que se convierten en púlsares giran a velocidades extremadamente altas debido a la conservación del momento angular. Al colapsar, el radio de la estrella disminuye significativamente, lo que reduce su momento de inercia y aumenta su velocidad angular.
Giroscopios
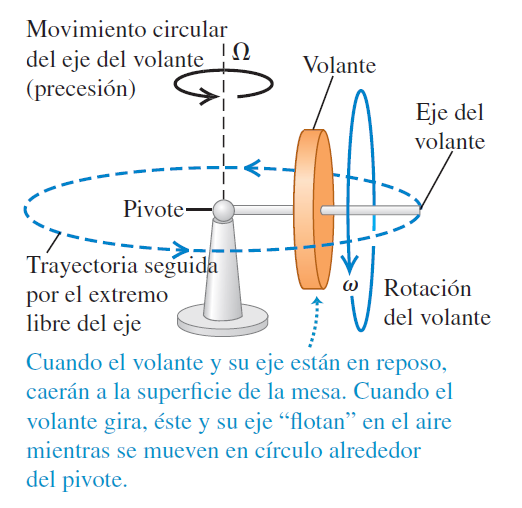
Un giroscopio es un dispositivo que utiliza el principio de conservación del momento angular para mantener su orientación. Consiste en un disco o rueda que gira rápidamente alrededor de su eje. Debido a la conservación del momento angular, el eje de un giroscopio permanecerá apuntando en la misma dirección, a menos que una torca externa actúe sobre él.
Los giroscopios se utilizan en una variedad de aplicaciones, desde juguetes y dispositivos electrónicos hasta sistemas de navegación en aviones y satélites. Su capacidad para mantener una orientación estable los hace ideales para estas aplicaciones.
La precesión es un fenómeno asociado con los giroscopios. Cuando se aplica una torca a un giroscopio, en lugar de cambiar su orientación directamente, el eje del giroscopio se desplaza perpendicularmente a la dirección de la torca aplicada. Este movimiento es conocido como precesión, y la velocidad de precesión se puede calcular utilizando la siguiente fórmula:
\( \Omega = \frac{\tau}{L} \)
Dónde:
- \( \Omega \) es la velocidad de precesión
- \( \tau \) es la torca aplicada
- \( L \) es el momento angular
Precesión
La precesión es el movimiento que describe el eje de un cuerpo rotatorio cuando se aplica una torca. En lugar de cambiar directamente su orientación, el eje del cuerpo se desplaza en un movimiento circular. La precesión es un fenómeno crucial en la dinámica de rotación y se observa en giroscopios y otros sistemas rotatorios.
Un ejemplo claro de precesión es un trompo que gira. Cuando el trompo empieza a perder velocidad, su eje comienza a describir un círculo en lugar de mantenerse vertical. Este movimiento de precesión se debe a la combinación de la gravedad y la rotación del trompo.
La precesión giroscópica tiene aplicaciones prácticas en la estabilización de aeronaves y naves espaciales. Los sistemas de control utilizan giroscopios para detectar y corregir cambios en la orientación, asegurando que la nave mantenga su rumbo.
Ejemplo de Cálculo de Torca
Para aflojar una junta de tubería, un plomero ensarta un pedazo de tubo (una “extensión”) en el mango de su llave. Se coloca de pie en el extremo del tubo, aplicando todo su peso de 900 N en un punto a 0.80 m del centro de la junta. El mango de la llave y la extensión forman un ángulo de 19° con la horizontal. Encuentre la magnitud y dirección de la torca que se aplica en torno al centro de la junta.
Solución:
\( \tau = F \cdot l \cdot \sin(\theta) \)
Donde:
- \( F = 900 \, \text{N} \)
- \( l = 0.80 \, \text{m} \)
- \( \theta = 19° \)
Calculando la torca:
\( \tau = 900 \, \text{N} \times 0.80 \, \text{m} \times \sin(19°) = 680 \, \text{N} \cdot \text{m} \)
Ejemplo de Momento Angular
Un patinador artístico gira sobre el hielo con los brazos extendidos. Su momento de inercia con los brazos extendidos es \( 5 \, \text{kg} \cdot \text{m}^2 \) y su velocidad angular es \( 2 \, \text{rad/s} \). ¿Cuál es su momento angular?
Solución:
\( L = I \omega \)
Donde:
- \( I = 5 \, \text{kg} \cdot \text{m}^2 \)
- \( \omega = 2 \, \text{rad/s} \)
Calculando el momento angular:
\( L = 5 \, \text{kg} \cdot \text{m}^2 \times 2 \, \text{rad/s} = 10 \, \text{kg} \cdot \text{m}^2 \cdot \text{rad/s} \)
Ejemplo de Precesión Giroscópica
Un giroscopio con un momento angular de \( 5 \, \text{kg} \cdot \text{m}^2 \cdot \text{rad/s} \) experimenta una torca de \( 2 \, \text{N} \cdot \text{m} \). ¿Cuál es la velocidad de precesión?
Solución:
\( \Omega = \frac{\tau}{L} \)
Donde:
- \( \Omega = \frac{2 \, \text{N} \cdot \text{m}}{5 \, \text{kg} \cdot \text{m}^2 \cdot \text{rad/s}} = 0.4 \, \text{rad/s} \)
Máquinas Simples
Son dispositivos que nos permiten realizar el mismo objetivo (trabajo) aplicando una menor fuerza.
Las máquinas simples son:
El plano inclinado.
Es una máquina simple que nos permite elevar cuerpos con una menor fuerza respecto a levantarla verticalmente.

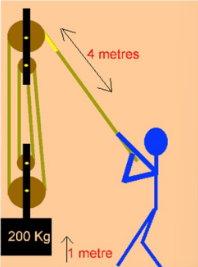
Poleas
Permite cambiar la dirección de la fuerza y en un sistema de poleas permite disminuir la fuerza aplicada.
Palancas
Nos permite disminuir la fuerza aplicada en la medida que se aumenta la distancia entre esta fuerza aplicada y el punto de apoyo. Se cumplen en las palancas las aplicaciones de torques respecto a un apoyo.

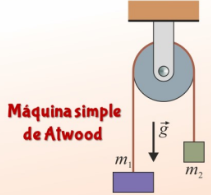
Máquina de Atwood
Es un dispositivo simple compuesto por una polea por la que se pasa una cuerda, de cuyos extremos penden dos masas.
Se usa en el laboratorio para calcular el valor de la aceleración de la gravedad, así como la aceleración y magnitud de la fuerza de fricción en la cuerda.
Aplicaciones Prácticas de la Dinámica de Rotación
La dinámica de rotación tiene numerosas aplicaciones prácticas en la ingeniería y la física. A continuación, se describen algunas de las más importantes:
1. Motores y Generadores Eléctricos
Los motores eléctricos convierten la energía eléctrica en energía mecánica rotacional, mientras que los generadores hacen lo opuesto. La comprensión de la torca y el momento angular es crucial para diseñar y optimizar estos dispositivos.
2. Rotores de Helicópteros
El diseño de los rotores de helicópteros depende de la dinámica de rotación. La estabilidad y el control de vuelo se logran mediante el ajuste preciso de la torca y el momento angular de los rotores.
3. Sistemas de Navegación Inercial
Los sistemas de navegación inercial utilizan giroscopios para mantener la orientación y la estabilidad de vehículos como aviones y submarinos. La precesión y la conservación del momento angular son principios clave en estos sistemas.
4. Equipos Deportivos
En deportes como el patinaje artístico y la gimnasia, los atletas utilizan la conservación del momento angular para realizar giros y saltos complejos. La comprensión de estos principios permite a los entrenadores y atletas mejorar su rendimiento.
5. Ingeniería Civil
En la construcción de puentes y edificios, se considera la torca y el momento angular para asegurar que las estructuras puedan soportar fuerzas externas como el viento y los terremotos.
6. Astrofísica
El estudio del movimiento de los planetas y las estrellas se basa en la dinámica de rotación. La conservación del momento angular explica fenómenos como la formación de sistemas planetarios y la evolución de las estrellas.

