

La segunda ley de la termodinámica es una de las leyes fundamentales de la física que describe la dirección de los procesos termodinámicos. Esta ley establece que ciertos procesos ocurren espontáneamente en una dirección y no en la inversa. Por ejemplo, el calor fluye de un cuerpo caliente a uno frío y no al revés. Esta ley también introduce el concepto de entropía, que mide el grado de desorden o aleatoriedad de un sistema.
La segunda ley de la termodinámica se puede enunciar de varias maneras, pero todas las formulaciones son equivalentes y conducen a la misma conclusión: la entropía del universo tiende a aumentar. Esta ley tiene implicaciones profundas en muchos campos, desde la ingeniería hasta la cosmología, y es esencial para comprender la eficiencia de las máquinas térmicas y la evolución de los sistemas naturales.
En este artículo, exploraremos en profundidad la segunda ley de la termodinámica, sus formulaciones, ejemplos prácticos, y su importancia en diversos campos de la ciencia y la ingeniería.

Existen varias formulaciones de la segunda ley de la termodinámica, cada una de las cuales proporciona una perspectiva diferente pero equivalente de esta ley fundamental. Algunas de las formulaciones más comunes incluyen:
El enunciado de Clausius establece que es imposible construir un dispositivo cuyo único efecto sea transferir calor de un cuerpo frío a uno caliente sin realizar trabajo sobre el dispositivo. En otras palabras, no es posible que el calor fluya espontáneamente de un cuerpo frío a uno caliente.
El enunciado de Kelvin-Planck establece que es imposible construir una máquina térmica que, operando en un ciclo, convierta todo el calor absorbido en trabajo. Siempre habrá una parte del calor que no se convierte en trabajo y se rechaza al entorno.
La segunda ley también puede formularse en términos de entropía. La entropía de un sistema aislado siempre aumenta o, en el mejor de los casos, permanece constante. Esto implica que los procesos naturales tienden a evolucionar hacia estados de mayor desorden.

Todos los procesos termodinámicos naturales son irreversibles. Esto significa que ocurren espontáneamente en una dirección pero no en la otra. Por ejemplo, cuando se desliza un libro sobre una mesa, la energía mecánica se convierte en calor debido a la fricción, y este proceso es irreversible.
La irreversibilidad de los procesos termodinámicos está relacionada con la producción de entropía. En un proceso irreversible, la entropía total del sistema y su entorno aumenta. Esto contrasta con los procesos reversibles ideales, en los cuales la entropía total permanece constante.
Un proceso reversible es un proceso idealizado que ocurre infinitamente lento, de manera que el sistema permanece en equilibrio termodinámico en todo momento. En la práctica, todos los procesos reales son irreversibles, pero los procesos reversibles son útiles como modelos teóricos para analizar la eficiencia de las máquinas térmicas.
Ejemplos de procesos irreversibles incluyen la expansión libre de un gas, la fricción, la disipación de energía en forma de calor, y las reacciones químicas espontáneas. Estos procesos aumentan la entropía del sistema y del entorno, y no pueden revertirse sin intervención externa.
A continuación se presentan algunos ejemplos comunes de procesos irreversibles:
Una máquina térmica convierte calor parcialmente en trabajo mecánico. Por lo general, una máquina térmica realiza un proceso cíclico en el que una sustancia de trabajo (como el aire y el combustible en un motor de combustión interna) experimenta entrada y salida de calor, expansión y compresión.
La eficiencia térmica de una máquina, denotada por \( e \), es la fracción del calor absorbido que se convierte en trabajo:
\[ e = \frac{W}{Q_H} = 1 - \frac{Q_C}{Q_H} \]
Donde \( Q_H \) es el calor absorbido del depósito caliente y \( Q_C \) es el calor rechazado al depósito frío.
Una máquina térmica ideal que opera de acuerdo con el ciclo de Carnot es la más eficiente posible. La eficiencia de una máquina de Carnot depende únicamente de las temperaturas de los depósitos caliente y frío:
\[ e_{Carnot} = 1 - \frac{T_C}{T_H} \]
Donde \( T_H \) es la temperatura del depósito caliente y \( T_C \) es la temperatura del depósito frío. Ninguna máquina real puede superar la eficiencia de una máquina de Carnot.
Las máquinas térmicas incluyen motores de combustión interna, motores de vapor, y turbinas de gas y vapor. Cada uno de estos dispositivos opera según ciclos termodinámicos específicos que determinan su eficiencia y su capacidad para realizar trabajo útil.
Existen varios tipos de máquinas térmicas, cada una con sus propias características y aplicaciones. A continuación se describen algunos de los tipos más comunes:
La eficiencia de las máquinas térmicas es una medida de cuán efectivamente convierten el calor en trabajo. La eficiencia de una máquina térmica se puede expresar como la relación entre el trabajo producido y el calor absorbido:
\[ e = \frac{W}{Q_H} \]
Donde \( W \) es el trabajo producido y \( Q_H \) es el calor absorbido. La eficiencia de una máquina térmica siempre será menor que uno debido a las pérdidas de calor y la producción de entropía.
La entropía es una medida del desorden de un sistema. La segunda ley de la termodinámica establece que la entropía de un sistema aislado siempre aumenta con el tiempo. Esto explica por qué ciertos procesos, como la mezcla de tinta con agua, no se revierten espontáneamente.
Matemáticamente, el cambio en la entropía \( \Delta S \) se puede expresar como:
\[ \Delta S = \int \frac{dQ}{T} \]
Donde \( dQ \) es el calor transferido y \( T \) es la temperatura del sistema.
El concepto de entropía es fundamental para la termodinámica y tiene implicaciones en muchos campos, desde la física hasta la teoría de la información. La segunda ley implica que el desorden en el universo tiende a aumentar, lo que tiene profundas implicaciones filosóficas y científicas.
En términos de eficiencia, la segunda ley establece que ninguna máquina térmica puede ser 100% eficiente, ya que siempre habrá una parte del calor que no se convierte en trabajo y se pierde como calor residual. Esta limitación fundamental está relacionada con el aumento de la entropía.
La entropía también juega un papel crucial en la teoría de la información, donde se utiliza para cuantificar la cantidad de incertidumbre o desorden en un conjunto de datos. En este contexto, la entropía mide la cantidad de información necesaria para describir un sistema o proceso.
A continuación se presentan algunos ejemplos que ilustran el concepto de entropía:
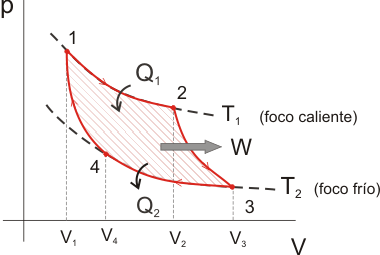
El ciclo de Carnot es un ciclo termodinámico ideal que proporciona la máxima eficiencia posible para una máquina térmica operando entre dos temperaturas. Consta de dos procesos isotérmicos y dos adiabáticos:
La eficiencia del ciclo de Carnot se expresa como:
\[ e_{Carnot} = 1 - \frac{T_C}{T_H} \]
Donde \( T_H \) es la temperatura del depósito caliente y \( T_C \) es la temperatura del depósito frío.
El ciclo de Carnot es útil como modelo teórico para comprender los límites de la eficiencia de las máquinas térmicas. Aunque ninguna máquina real puede operar exactamente según el ciclo de Carnot, este ciclo proporciona un estándar contra el cual se pueden comparar las máquinas reales.
El ciclo de Carnot consiste en los siguientes pasos:
El ciclo de Carnot ilustra los principios fundamentales de la termodinámica y proporciona una base para el diseño y análisis de máquinas térmicas eficientes.
El ciclo de Carnot se utiliza como modelo teórico para evaluar la eficiencia de las máquinas térmicas. Aunque ninguna máquina real puede operar exactamente según el ciclo de Carnot, este ciclo proporciona un límite superior para la eficiencia de las máquinas térmicas reales. Algunas aplicaciones incluyen:
Para comprender mejor la segunda ley de la termodinámica, es útil ver algunos ejemplos prácticos de cómo se aplica esta ley en diferentes situaciones:
Un motor de combustión interna toma 10,000 J de calor y produce 2,000 J de trabajo mecánico por ciclo. El calor se obtiene quemando gasolina. La eficiencia térmica del motor es:
\[ e = \frac{W}{Q_H} = \frac{2000 \, \text{J}}{10000 \, \text{J}} = 0.20 = 20\% \]
El calor rechazado en cada ciclo es:
\[ Q_C = Q_H - W = 10000 \, \text{J} - 2000 \, \text{J} = 8000 \, \text{J} \]
La potencia de salida desarrollada en watts y en caballos de fuerza (hp) si el motor realiza 25 ciclos por segundo es:
\[
P = W \times \text{ciclos/segundo} \]
\[ =2000 \, \text{J} \times 25 \, \text{ciclos/segundo} \]
\[= 50,000 \, \text{W} = 67 \, \text{hp}
\]
Un refrigerador toma 500 J de calor del interior y expulsa 700 J al exterior. El trabajo realizado por el refrigerador es:
\[ W = Q_H - Q_C = 700 \, \text{J} - 500 \, \text{J} = 200 \, \text{J} \]
El coeficiente de rendimiento (COP) del refrigerador es:
\[ COP = \frac{Q_C}{W} = \frac{500 \, \text{J}}{200 \, \text{J}} = 2.5 \]
Un calentador de agua toma 3,000 J de calor y transfiere 2,500 J al agua. La eficiencia del calentador es:
\[ e = \frac{Q_C}{Q_H} = \frac{2500 \, \text{J}}{3000 \, \text{J}} = 0.833 = 83.3\% \]
Una planta de energía convierte 50,000 J de calor en 20,000 J de trabajo mecánico. La eficiencia de la planta es:
\[ e = \frac{W}{Q_H} = \frac{20000 \, \text{J}}{50000 \, \text{J}} = 0.4 = 40\% \]
El calor rechazado es:
\[ Q_C = Q_H - W = 50000 \, \text{J} - 20000 \, \text{J} = 30000 \, \text{J} \]
La segunda ley de la termodinámica establece que en cualquier proceso espontáneo, la entropía total del sistema y su entorno siempre aumenta. Esta ley tiene varias implicaciones importantes:
La segunda ley de la termodinámica es una de las leyes fundamentales de la naturaleza y tiene aplicaciones en una amplia variedad de campos, desde la ingeniería hasta la cosmología. Comprender esta ley es esencial para el estudio de la física y la ingeniería térmica.
La segunda ley también explica fenómenos cotidianos, como por qué el hielo se derrite en un vaso de agua caliente, por qué los motores de los automóviles no pueden convertir toda la energía del combustible en trabajo útil, y por qué los seres vivos necesitan consumir energía para mantener su organización interna.
La segunda ley de la termodinámica nos proporciona una comprensión profunda de la dirección y la eficiencia de los procesos termodinámicos. Nos enseña que todos los procesos naturales tienden a aumentar el desorden del universo y que la eficiencia de las máquinas térmicas siempre estará limitada por esta ley fundamental.
El estudio de la termodinámica y, en particular, de la segunda ley, es esencial para muchas disciplinas, desde la ingeniería y la física hasta la biología y la informática. Al comprender y aplicar esta ley, podemos diseñar sistemas más eficientes y sostenibles, y entender mejor el funcionamiento del universo.
En resumen, la segunda ley de la termodinámica es una piedra angular de la ciencia moderna que influye en nuestra comprensión del mundo y en el desarrollo de tecnologías avanzadas.
Para finalizar, recordemos las palabras de Sadi Carnot, uno de los padres de la termodinámica: "La naturaleza nos ha dado una máquina térmica ideal; nuestra tarea es aprender a usarla de la mejor manera posible."