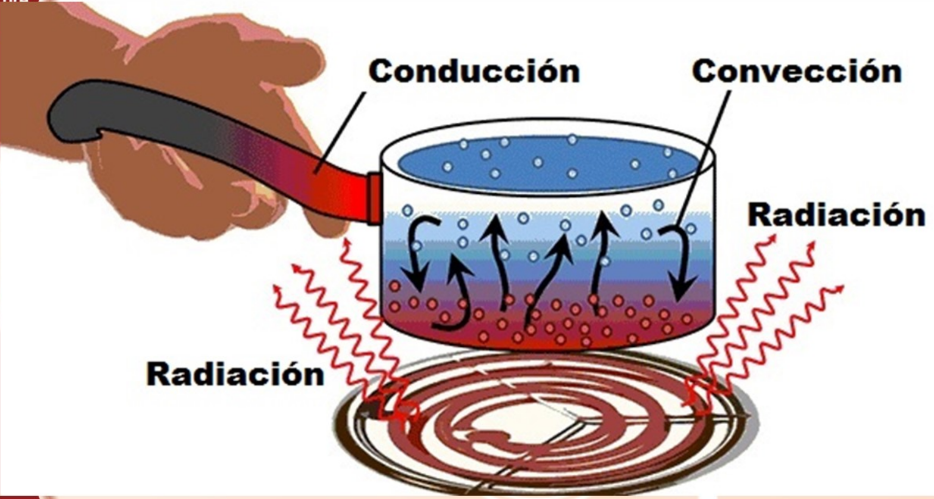
La termodinámica es el estudio de la energía, el calor y el trabajo, y cómo interactúan en varios sistemas. Por ejemplo, en el motor de un automóvil, se genera calor por la reacción química entre el oxígeno y la gasolina vaporizada en sus cilindros. El gas caliente empuja los pistones de los cilindros, efectuando trabajo mecánico que se utiliza para impulsar el vehículo. Este es un ejemplo de proceso termodinámico.
La primera ley de la termodinámica resulta fundamental para entender estos procesos y es una extensión del principio de conservación de la energía. Dicha ley amplía este principio para incluir el intercambio de energía tanto por transferencia de calor como por trabajo mecánico, e introduce el concepto de la energía interna de un sistema. La conservación de la energía desempeña un papel vital en todas las áreas de la física, en tanto que la primera ley de la termodinámica tiene una utilidad muy amplia.
Para plantear las relaciones de energía con precisión, necesitaremos el concepto de sistema termodinámico, y estudiaremos el calor y el trabajo como dos formas de introducir energía en tal sistema o de extraerla de él.

Ya estudiamos la transferencia de energía mediante trabajo mecánico y por transferencia de calor. Ahora podemos combinar y generalizar estos principios.
Siempre hablaremos de transferencia de energía hacia o desde algún sistema específico. El sistema podría ser un dispositivo mecánico, un organismo biológico o cierta cantidad de material como el refrigerante de un acondicionador de aire o el vapor de agua que se expande en una turbina. En general, un sistema termodinámico es cualquier conjunto de objetos que conviene considerar como una unidad, y que podría intercambiar energía con el entorno. Un ejemplo conocido es una cantidad de granos de maíz para elaborar rosetas en una olla con tapa. Al colocarse la olla sobre una estufa, se agrega energía al maíz por conducción de calor. Al reventarse el maíz y expandirse, realiza trabajo ejerciendo una fuerza hacia arriba sobre la tapa y la desplaza.
En mecánica, a menudo usamos el concepto de sistema en relación con los diagramas de cuerpo libre, y la conservación de la energía y la cantidad de movimiento o momento. En los sistemas termodinámicos, al igual que en todos los demás, es indispensable definir con claridad desde un principio exactamente lo que está incluido en el sistema y lo que no. Sólo así podremos describir sin ambigüedad las transferencias de energía al sistema y desde éste.
La termodinámica tiene sus raíces en muchos problemas prácticos además del inflado del maíz para elaborar rosetas. El motor de gasolina en un automóvil, los motores a reacción de un avión y los motores de los cohetes de lanzamiento usan el calor de la combustión del combustible para realizar trabajo mecánico e impulsar el vehículo. El tejido muscular de los organismos vivos metaboliza la energía química del alimento y realiza trabajo mecánico sobre el entorno del organismo. Una máquina o una turbina de vapor usa el calor de combustión del carbón u otro combustible para realizar trabajo mecánico, como al impulsar un generador eléctrico o impulsar un tren.
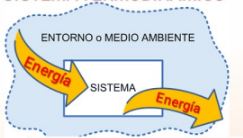
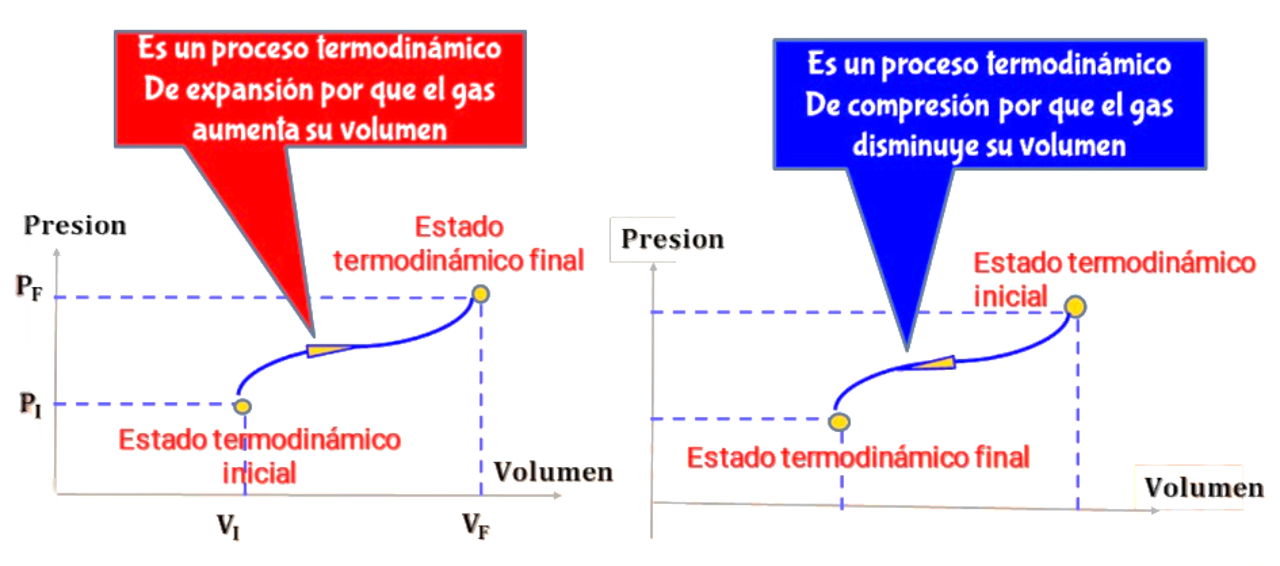
Una cantidad de gas en un cilindro con un pistón móvil es un ejemplo sencillo de sistema termodinámico. Los motores de combustión interna, las máquinas de vapor, y las compresoras de refrigeradores y acondicionadores de aire usan alguna versión de este tipo de sistema. En las siguientes secciones emplearemos el sistema de gas en un cilindro para explorar varios tipos de procesos termodinámicos.
Podemos entender el trabajo efectuado por un gas en un cambio de volumen considerando sus moléculas. Cuando una de ellas choca contra una superficie estacionaria, ejerce una fuerza momentánea sobre ella pero no realiza trabajo porque la superficie no se mueve. En cambio, si la superficie se mueve, como un pistón de un motor de gasolina, la molécula sí realiza trabajo sobre la superficie durante el choque.
La ecuación para el trabajo realizado durante un cambio de volumen es:
\[ dW = p dV \]
En un cambio finito de volumen de \( V_1 \) a \( V_2 \), el trabajo realizado es:
\[ W = \int_{V_1}^{V_2} p \, dV \]
En general, la presión del sistema puede variar durante un cambio de volumen; por ejemplo, en los cilindros de un motor de automóvil durante el movimiento hacia arriba y hacia abajo de los pistones. Para evaluar esta integral, hay que saber cómo varía la presión en función del volumen. Podemos representar esta relación en una gráfica de \( p \) en función de \( V \).
De acuerdo con la regla planteada, el trabajo es positivo cuando el sistema se expande. En una expansión del estado 1 al 2, el área bajo la curva y el trabajo son positivos. Una compresión de 1 a 2 da un área negativa; cuando un sistema se comprime, su volumen disminuye y realiza trabajo negativo sobre su entorno.
Si la presión \( p \) permanece constante mientras el volumen cambia de \( V_1 \) a \( V_2 \), el trabajo efectuado por el sistema es:
\[ W = p (V_2 - V_1) \]
Hemos visto que, si un proceso termodinámico implica un cambio de volumen, el sistema realiza trabajo (positivo o negativo) sobre su entorno. También entrará o saldrá calor del sistema durante el proceso si hay una diferencia de temperatura entre el sistema y su entorno. Veamos ahora cómo el trabajo efectuado por el sistema y el calor agregado a éste durante un proceso termodinámico dependen de la forma en que se realiza el proceso.
Cuando un sistema termodinámico cambia de un estado inicial a uno final, pasa por una serie de estados intermedios, a los que llamamos trayectoria. Siempre hay un número infinito de posibilidades para dichos estados intermedios. Si todos son estados de equilibrio, la trayectoria podrá representarse en un diagrama \( pV \). El punto 1 representa un estado inicial con presión \( p_1 \) y volumen \( V_1 \), y el punto 2 representa un estado final con presión \( p_2 \) y volumen \( V_2 \).
Para pasar del estado 1 al 2, podríamos mantener la presión constante en \( p_1 \) mientras el sistema se expande al volumen \( V_2 \), y luego reducir la presión a \( p_2 \) mientras se mantiene el volumen en \( V_2 \). El trabajo efectuado por el sistema durante este proceso es el área bajo la línea 1 S 3; no se efectúa trabajo durante el proceso a volumen constante 3 S 2.
Otra posibilidad es seguir la trayectoria 1 S 4 S 2; en tal caso, el trabajo es el área bajo la línea 4 S 2, ya que no se efectúa trabajo durante el proceso a volumen constante 1 S 4. La curva continua de 1 a 2 es otra posibilidad, y el trabajo para esta trayectoria es diferente del que se realiza en cualquiera de las otras.
Concluimos que el trabajo realizado por el sistema depende no sólo de los estados inicial y final, sino también de los estados intermedios, es decir, de la trayectoria.
La energía interna es uno de los conceptos más importantes de la termodinámica. En la sección 7.3, cuando hablamos de los cambios de energía de un cuerpo que se desliza con fricción, mencionamos que calentar un cuerpo aumentaba su energía interna y que enfriarlo la disminuía. Pero, ¿qué es energía interna? Podemos verla de varios modos; comencemos con uno basado en las ideas de la mecánica. La materia consiste en átomos y moléculas, y éstos se componen de partículas que tienen energías cinética y potencial. Definimos tentativamente la energía interna de un sistema como la suma de las energías cinéticas de todas sus partículas constitutivas, más la suma de todas las energías potenciales de interacción entre ellas.
En un proceso cíclico, el estado final es igual que el inicial, por lo que el cambio total de energía interna debe ser cero. Entonces, \( \Delta U = 0 \) y \( Q = W \). Si el sistema realiza una cantidad neta de trabajo \( W \) durante este proceso, deberá haber entrado en el sistema una cantidad igual de energía como calor \( Q \).
Un proceso cíclico es uno en el que el sistema pasa por varios estados, pero finalmente regresa a su estado original, de manera que sus propiedades (presión, volumen, temperatura) son las mismas que al principio. El primer ejemplo que se nos viene a la mente es un motor térmico, que utiliza calor para realizar trabajo.
Describimos cuatro clases específicas de procesos termodinámicos que ocurren con frecuencia en situaciones prácticas:
La figura 19.16 muestra una gráfica \( pV \) para cada uno de estos cuatro procesos con una cantidad constante de gas ideal. La trayectoria seguida en un proceso adiabático se llama adiabática. Una línea vertical (volumen constante) es una isocórica; una línea horizontal (presión constante) es una isobárica; y una curva de temperatura constante es una isoterma.
En un proceso adiabático no hay transferencia de calor (\( Q = 0 \)). Esto puede lograrse aislando térmicamente el sistema de su entorno, o haciendo que el proceso sea tan rápido que no haya tiempo para la transferencia de calor. En este caso, la primera ley de la termodinámica se reduce a \( \Delta U = -W \).
Un ejemplo de proceso adiabático es la expansión rápida de un gas en un cilindro aislado. A medida que el gas se expande, realiza trabajo sobre el pistón, y su energía interna disminuye, lo que resulta en una disminución de la temperatura del gas.
En un proceso isocórico, el volumen del sistema permanece constante (\( \Delta V = 0 \)), por lo que no se realiza trabajo (\( W = 0 \)). La primera ley de la termodinámica se reduce a \( \Delta U = Q \). Toda la energía agregada al sistema como calor se utiliza para aumentar su energía interna.
Un ejemplo de proceso isocórico es calentar un gas en un recipiente rígido y cerrado. A medida que se agrega calor al gas, su temperatura y presión aumentan, pero su volumen permanece constante.
En un proceso isobárico, la presión del sistema permanece constante. El trabajo realizado por el sistema es \( W = p \Delta V \). La primera ley de la termodinámica se expresa como \( \Delta U = Q - p \Delta V \).
Un ejemplo de proceso isobárico es calentar un gas en un cilindro con un pistón que puede moverse libremente. A medida que se agrega calor al gas, su volumen aumenta mientras la presión permanece constante.
En un proceso isotérmico, la temperatura del sistema permanece constante (\( \Delta T = 0 \)). Para un gas ideal, esto significa que la energía interna también permanece constante (\( \Delta U = 0 \)). La primera ley de la termodinámica se reduce a \( Q = W \).
Un ejemplo de proceso isotérmico es la compresión lenta de un gas en un cilindro a temperatura constante. A medida que el gas se comprime, se libera una cantidad equivalente de calor para mantener la temperatura constante.
Para un gas ideal, la energía interna depende solo de la temperatura, no de la presión ni del volumen. La ecuación de estado del gas ideal es:
\[ pV = nRT \]
La energía interna \( U \) de un gas ideal es una función de la temperatura \( T \) solamente. Esto se puede expresar como:
\[ U = f(T) \]
Muchos experimentos han demostrado que, cuando un gas de baja densidad (en esencia, un gas ideal) sufre una expansión libre, su temperatura no cambia. La conclusión es: La energía interna \( U \) de un gas ideal depende sólo de su temperatura, no de su presión ni de su volumen.
En el caso de los gases que no se comportan como gas ideal, hay cambios de temperatura durante las expansiones libres, aunque la energía interna sea constante. Ello indica que la energía interna no puede depender sólo de la temperatura; debe depender también de la presión.
Consideremos la ecuación de estado de un gas ideal \( pV = nRT \). Si un gas ideal se expande de un volumen inicial \( V_1 \) a un volumen final \( V_2 \) a temperatura constante \( T \), podemos calcular el trabajo realizado por el gas usando la integral:
\[ W = \int_{V_1}^{V_2} p \, dV \]
Para un proceso isotérmico, podemos expresar la presión en términos del volumen y la temperatura usando la ecuación de estado:
\[ p = \frac{nRT}{V} \]
Entonces, el trabajo realizado por el gas durante una expansión isotérmica es:
\[ W = \int_{V_1}^{V_2} \frac{nRT}{V} \, dV = nRT \ln \frac{V_2}{V_1} \]
En un proceso adiabático, la relación entre la presión y el volumen de un gas ideal está dada por la ecuación de Poisson:
\[ pV^\gamma = \text{constante} \]
donde \( \gamma \) es la relación de capacidades caloríficas \( \gamma = \frac{C_p}{C_v} \). Para un proceso adiabático reversible, podemos usar esta relación para encontrar el trabajo realizado por el gas.